快速排序图解
故事开始了
假设有这样一个场景,有个小学生给了你10000个数字,要你在一天之内把这些数字排好序,然后交给他.身为一个程序猿,你想到了排序算法,进而又想到了快速排序.那么快速排序是怎么实现的呢?
既然10000个数字能排序,那么6个数字也能排序,只要6个数字时,运行结果是准确的,那么这个排序算法就能通用任意个数字的排序.假设我们有这么6个数字:
3 7 2 1 4 6 .首先,快速排序要找个基准点,一般是开头的数字,在我们这个例子中是3,然后想办法把3放到数列的中间位置,使得左边的数字比3小,右边的数字比3大,然后再递归3左右两边的数组,继续使用快速排序,最后就能全局排序.所以要搞清楚,有什么办法可以做到我们要的效果.一个可行的方法是这样的:在数组的头部和尾部各放置一个指针,然后让尾巴和3进行比较,如果大于等于3,那么就往左移动,如果碰到了比3大的数,那么就停下来.另外,如果碰到了左边的指针,也要停下来,这说明我们要的效果已经达到了.说这么多,可能还不够直观,我们用图的方式来模拟这个过程.
起初,整个指针的位置是这样的:
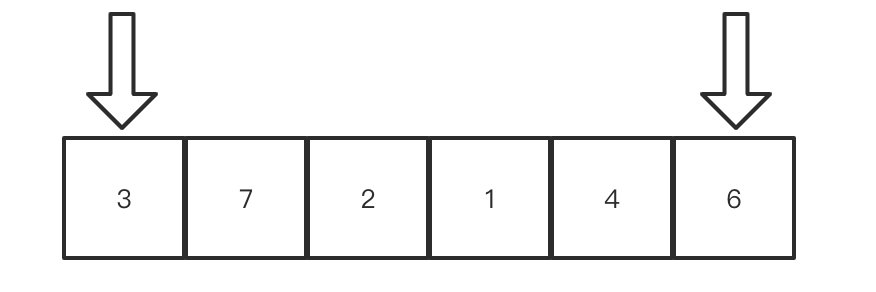
指针继续向左移动,6比3大,4也比3大,直到遇到了1,比3小,这个时候右边的指针就停下来,并且在移动过程中并未碰到左边的指针.现在指针的位置是这样的:
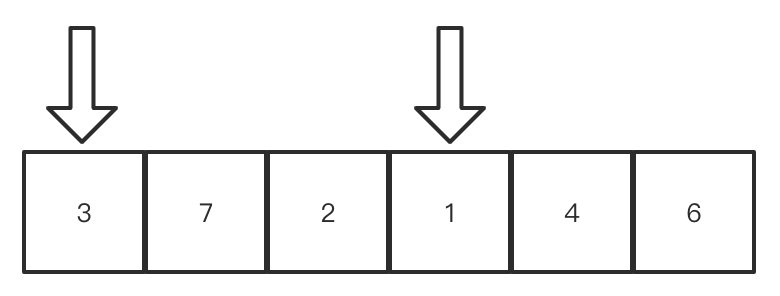
同理,左边的指针如果小于等于3,也要向右移动,直到遇到比3大的数,或者遇到了右指针也要停下来.3等于3,向右移动,7大于3,停下来,现在指针的位置是这样的:
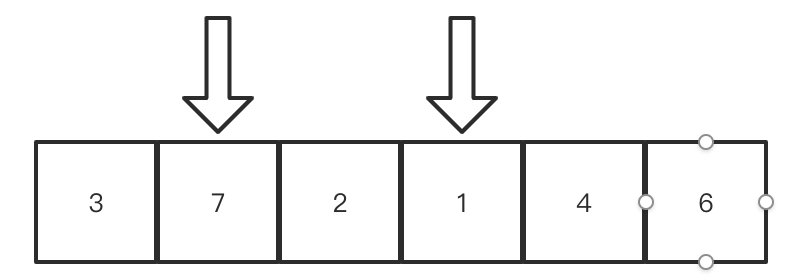
此时,我们把两个指针所指的数字交换一下,为什么要交换呢?因为我们要使得左边的数比3小,右边的数比3大,然后就形成了下面这张图:
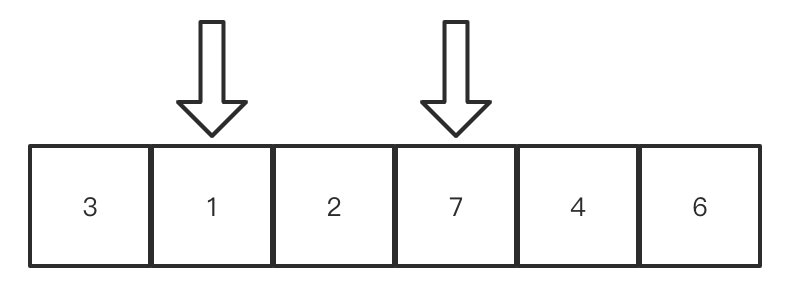
此时,两个指针还未碰到,但是我们能看到的是:右指针右边的数据全部比3大,左指针左边的数字全部比3小.这是一个很直观的现象.
接着,我们继续移动右指针,这里的7还要和3再比较一次,当然肯定是比3大,所以一定会左移.然后2比3小,右指针又停下来了:
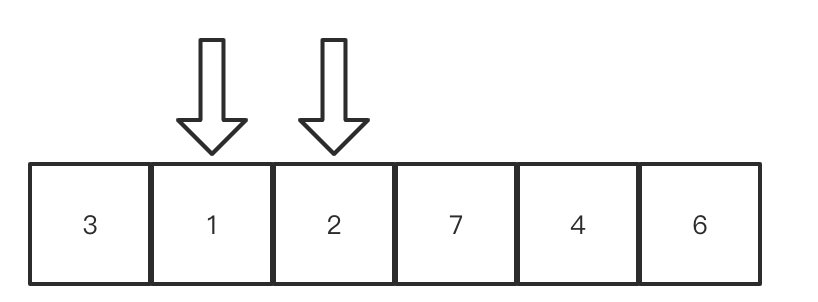
然后左指针用1和3比,肯定要向右移动,然后移动过去时,发现碰到了右指针:
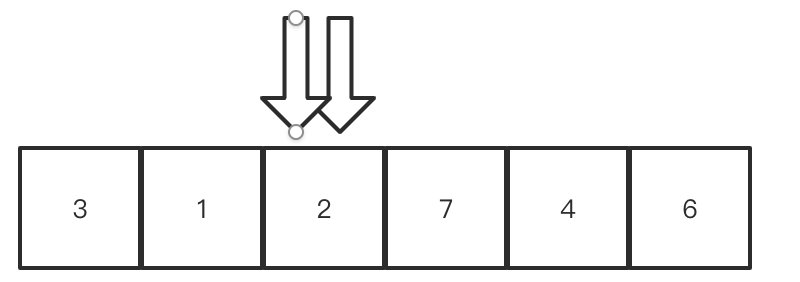
它们撞到一起去了,这个时候我们已经达到了我们的目的,这就是左右指针停下来的一个标志,我们把开头的3和此时这个位置上的2进行一个交换,那么就变成了:
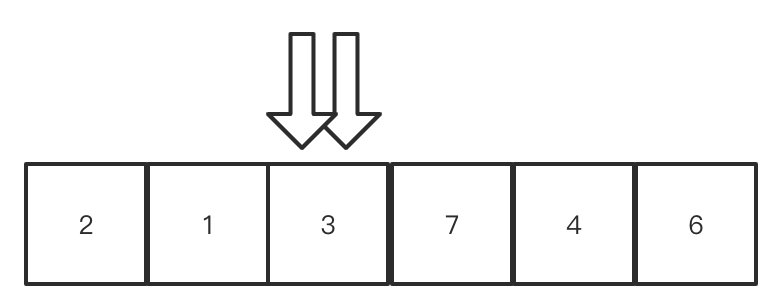
卧槽!我们达到我们的终极目的:使得3左边的数字比3小,右边的数字比3大.
接下来的故事是,保持3这个位置不动,将左边的2,1当成一个数组,右边的7,4,6当成一个数组,然后再重新对每个数组搞两个指针进行移动,切记:撞到了就是成功了.那么我们可以使用递归的方式来做剩余的事情.如果数组只剩下一个元素,那么一定要结束递归,此时的结束条件是i>=j.下面将展示快速排序的代码,也就是模拟我们现在的整个过程.
快速排序代码
1 | |
首先代码的开始是判断是不是要结束递归,紧接着,搞出两个指针,开始和开头位置的数字进行比较.代码里面始终要判断i<j,因为撞到了就是成功了,无需再进行下去,另外再没撞到之前,如果双方都停下来一次之后,要交换一下所指的数字,这是为了确保右边的数字比开头的数字大,左边的数字比开头的数字小.
然后,如果i和j相遇,那么一次完整的快速排序就结束了,在遇到的地方和开头的数字进行一次交换,接着再进行左右两个数组的排序,如此递归下去,直到排完.
故事的最后
你轻轻松松的排完了10000个数字,写下代码的过程只用了59秒,接着你拿起了桌上那瓶95年的可乐喝了一口,顺手掏出了手机,开始刷起了你养了多年的B站号,进入了传说中的工作休息区.
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!